合作客戶/
拜耳公司 |
同濟大學 |
聯合大學 |
美國保潔 |
美國強生 |
瑞士羅氏 |
相關新聞Info
微凝膠顆粒在氣液界面處吸附動力學及動態方程研究——結果與討論
來源:上海謂載 瀏覽 1188 次 發布時間:2021-10-21
四、結果與討論
壓力面積等溫線是通過壓縮獲得 在朗繆爾槽上涂抹單層膜,用于 3 組不同的 實驗。 這些等溫線中的區域坐標被縮放 由吸附在界面上的顆粒數量決定。 一切 曲線折疊成單個圖,如圖 1 所示。 增加壓縮,壓力最初變化很小,但 每個顆粒低于 2 mm2,壓力會急劇增加。 曲線的斜率首先增加,但達到 最大在 ~27 mN m- 1 處有一個拐點 其次是稍弱的斜率。 面積值 對應于該拐點的粒子 (Ac) 結果為 為 0.545 mm2,如圖 1 中的虛線所示。假設 顆粒緊密堆積,這對應于~835 nm 的顆粒間距離,遠大于 在本體中測量的顆粒的流體動力學直徑 溶液 (590 nm) 表明顆粒確實是 大幅度變形。 如圖 1 的插圖所示,有限 0.5 mN m- 1 級的表面壓力(即遠高于我們的 檢測限為 0.1 mN m- 1 ) 事實上已經可以測量了 每個粒子的面積約為 4 mm2 . 插圖還表明 P 的絕對值可再現在 0.3 mN m- 1 以內 在兩個不同朗繆爾的不同實驗之間 槽。
在圖 2 中,我們展示了與圖 1 相同的數據,但轉換了 使用 G ? 1/(A * NAv) 繪制壓力與吸附量曲線 其中 A 是圖 1 中每個粒子的面積,NAv 是阿伏伽德羅數。 這條曲線代表了二維狀態方程 (EOS) 本系統。 在相對較低的密度 (<5 * 10- 13 摩爾米- 2 ) 壓力極低 (z1 mN m- 1 ) 但 相當好檢測。 因此,即使在低密度下, 粒子間距離遠大于溶液中的粒子大小,粒子仍然以某種方式相互作用。 作為粒子 幾乎沒有任何電泳遷移率,22,23 靜電 排斥不太可能是原因。 唯一的其他選擇是 顆粒-顆粒接觸。 因此粒子必須強 吸附在界面上時發生變形,即 定性地同意其他作者的發現。2,3,7,8,15,24 我們可以粗略估計變形的程度 ansatz Dr z Dg/3。 使用 3 z 50 kPa 的典型值 文獻 25,26 以及 Dg ? 70 mN m- 1 , 我們發現 ? 博士 1.7 毫米,與約 3 毫米之間的距離一致 密堆積和完全變形的顆粒。 我們基于我們的分析 假設我們傳播的粒子 界面不解吸。 但即使我們考慮了解吸 粒子,這只會意味著有限的壓力 檢測到的實際上對應于更低的表面 濃度。 圖3顯示了界面處顆粒變形機制的示意圖。 它 應該注意的是,在 LB 實驗的情況下,粒子是 散布在界面上,我們沒有任何粒子 大部分。 在界面張力測量的情況下, 粒子從本體擴散到界面。
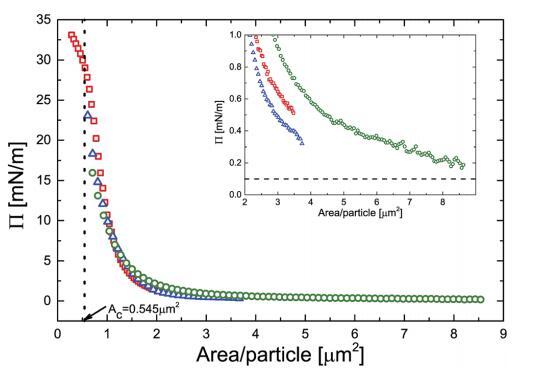
圖 1 PNIPAM 顆粒在空氣-水中的壓力面積等溫線 界面。 空心符號表示對應于三組不同實驗的實驗數據點,即: (,) NIMA 具有高初始顆粒負載的槽,(B) 具有低初始顆粒負載的 NIMA 槽 初始粒子負載和 (D) Kibron m-trough 具有高初始粒子 加載。 插圖顯示了低壓力區域曲線的擴展視圖 負荷。 插圖中的虛線表示檢測限 壓力傳感器。
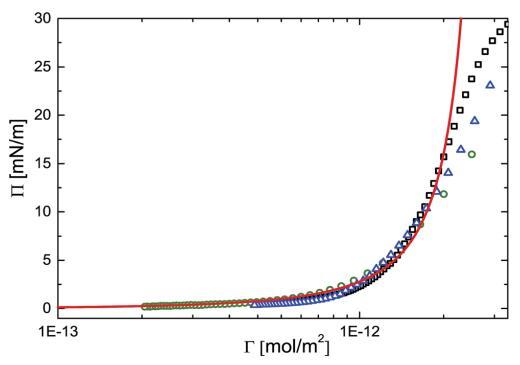
圖 2 表面壓力(P)與吸附的 PNIPAM 顆粒量 (G) 在空氣-水界面上。 開放符號表示實驗 對應于三組不同實驗的數據點 即:(,)具有高初始粒子負載的 NIMA 槽,(B)NIMA 低初始粒子負載的槽和 (D) Kibron m 槽 高初始粒子負載。 紅色實線表示預測 使用 Groot 和 Stoyanov 模型制作。
吸附在流體-流體界面上的粒子與 并產生表面壓力 (P),即 3D 系統中壓力的 2D 模擬。 通過擴展這個 進一步類比,也可以將這個表面壓力聯系起來 通過狀態方程到其他狀態參數,如數密度和溫度。 用于吸附膠體顆粒 在流體-流體界面上,最簡單的近似可能是 2D硬盤。 狀態方程 (EOS) 為一個 組件系統根據密度相關性給出 壓縮系數 Z。文獻中充滿了 提供表達的多種方法 EOS 2D 硬盤液。 Mulero 等人 27,28 提供了一個簡潔的 回顧和比較所有這些狀態方程。
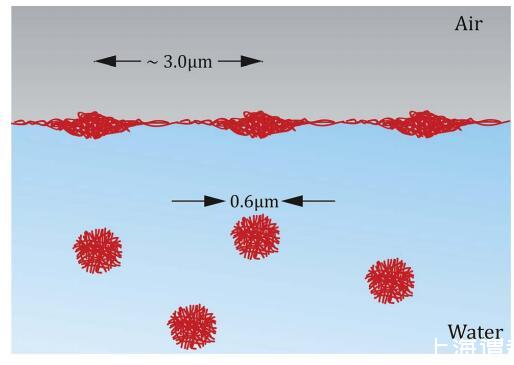
圖3 微凝膠變形示意圖 顆粒在非常低的負載下吸附到界面上 狀況。
我們發現在非常低的密度下,表面壓力 測量值至少高出 5-6 個數量級 假設在這些密度下是非相互作用粒子的理想氣體,對表面壓力的預測。 Groot 和 Stoyanov13 做 由于沒有明確考慮這些粒子的變形 表面張力。 他們只是假設壓力 主要取決于膠體顆粒內聚合物的微觀結構和組成,并引入 新的長度尺度 deff 旨在反映顆粒微觀結構,并將壓力放大到實驗 值。 然而,意識到粒子擴散到一個大 在某種程度上,我們還可以看到測量的壓力反映了 顆粒的內部彈性。 由于這是由 2D 給出的 交聯的密度,我們發現微觀長度也就不足為奇了。
Groot 和 Stoyanov 提出了表面壓力 (P) 的表達式,該表達式考慮了粒子內這些較小相關域的大小,由下式給出:
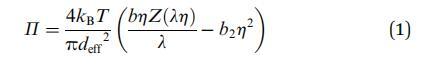
其中,diff 是相關域的大小 粒子。 壓縮系數 (Z) 可以表示為 使用文獻中可用的任何狀態方程。 在我們的 在這種情況下,我們使用修改后的亨德森方程 29 給出:
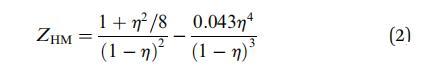
其中 h 是表面堆積分數,它可以反過來 用粒子數密度 (r) 和 單個顆粒的體積直徑 (d) 作為 h ? (p/4)rd2 . 對于我們的 實驗中,h 介于 0 和 0.91 之間。 相應的 ZHM 的值介于 1 到 96 之間。 我們將 Groot 和 Stoyanov 給出的比例關系擬合到我們的 圖2中的數據(紅色曲線)。 擬合給出了 deff ? 1.25 nm 作為 特征長度尺度。 為了提供實物圖片,這 deff 可以看作是交聯之間的平均距離 微凝膠顆粒內。 這與之前的一致 研究 30,31 報告了 1-10 nm 范圍內的網格尺寸。 模型中使用的參數 b 和 l 表示由于圓盤的彈性性質而產生的排斥相互作用。 對于我們的系統, b 和 l 的值可以統一。13 參數 b2 表示短程有吸引力的相互作用。 我們檢查了 通過結合短距離吸引相互作用的影響 參數 b2 作為擬合參數,但分析產生極 b2 的小值(~1 * 10-4 次方)。 因此我們得出結論,我們有 純排斥粒子。 與實際數據的偏差 高負載的模型可能是因為在高 壓縮,表面不再保持平坦,而是經歷 平面外變形,即彎曲。 還有這些顆粒 有很多松散的、未交聯的聚合物鏈段 沿著這些粒子的外圍。 在高壓縮時,它 積極地有利于這些細分市場離開 接口而不是相互滲透。 這種部分解吸 也可能導致與硬盤預測的偏差 喜歡模型。
已經建立了一個狀態方程來關聯 表面壓力和吸附量,我們現在繼續 研究顆粒的吸附動力學。 為此我們 監測新鮮的界面張力的演變 在 PNIPAM 顆粒懸浮液中制備氣泡作為 時間的函數。 我們轉換界面張力值 轉化為表面壓力。 結果如圖 4 所示。 表面壓力值最初迅速增加,然后 放松到最終的平衡值。 動態可以一目了然 分為兩個獨立的時間尺度:初始快速 由表面壓力增加表示的動力學 值,以及隨著系統向最終放松而緩慢的部分 平衡狀態。 快速動力學之間的這種區別 短時間和長時間慢得多的動力學是許多表面活性物質的吸附行為的特征 材料.32,33
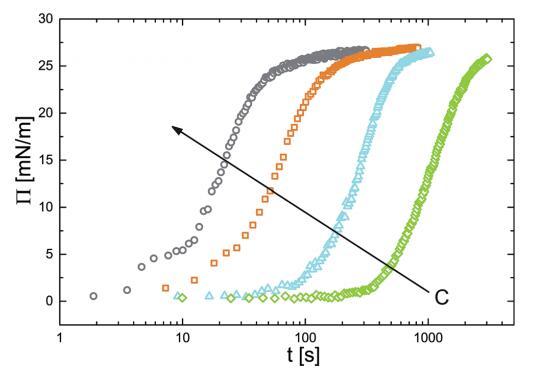
圖 4 表面壓力 (P) 隨時間的演變。 這 空心符號是實驗數據點。 不同的符號和 顏色表示顆粒的各種體積濃度:(>)0.10 g l-1 ,(四) 0.20 克 l-1 , (,)0.50 克 l- 1 , (B)1.00 克 l-1 . 箭頭表示方向 增加濃度。
在短時間尺度上,P 的增加受到 顆粒從主體到界面的傳輸。 我們 預計傳輸受粒子擴散控制。 由于我們的粒子相當大,吸附能為 這些粒子比 kBT 高 3-4 個數量級。 因此可以安全地假設粒子永遠不會離開 吸附后的界面。 在這些條件下, Ward 和 Tordai 模型 34 給出:

其中,G 是吸附摩爾質量,C 是體積濃度,D 是顆粒的擴散系數。
使用圖 2 中獲得的實驗 P 與 G 曲線,我們 將 P(t) 數據轉換為 G(t) 數據,然后將 G 與 Ct1/2 繪制為 如圖 5 所示。我們用濃度縮放時間軸 期望曲線折疊成一條曲線。 我們什么 觀察到 G 的初始增長遵循 t 1/2 依賴性很好。 其次是濃度依賴性 隨著系統長時間放慢 G 的弛豫 接近飽和。 圖 5 中的插圖顯示了個體 不同顆粒濃度的 G 與 t1/2 曲線。 這 實線是擬合實驗數據初始部分的直線(空心符號)。 每條曲線的初始斜率 產生擴散系數 D 的值。為了比較, 虛線是用 D 計算的斜率繪制的 從動態光散射 (DLS) (DDLS ? 7.29 * 10- 13 平方米 s- 1 )。 可以看出,它們的偏差不大 從實驗曲線。 或者,我們可以確定 D 從最佳擬合到數據。 表 1 給出了 D 的值 通過將直線(實線)擬合到不同體積濃度的實驗結果并比較 從 DLS 獲得的值。 如此獲得的值做 與 DLS 測量值的偏差不超過 10%。
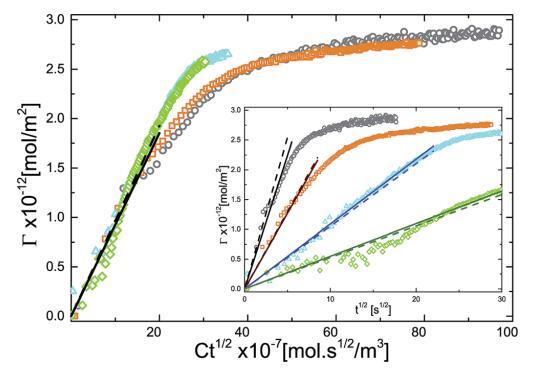
圖 5 吸附量 (G) 作為乘積 Ct1/2 的函數。 這 插圖顯示了不同體積的 G 與 t1/2 的單獨曲線 微凝膠顆粒濃度:(>)0.10 g l-1 , (D)0.20 克 l-1 , (,) 0.50 克 l-1 , (B)1.00 克 l-1 . 實線是直線擬合和虛線 用使用 D ? DDLS 計算的斜率繪制。
表 1 擴散系數 D (m2 s- 1 ) 對于各種 從實驗 G vs. t1/2 曲線計算的濃度 與使用 DLS 測量的相比

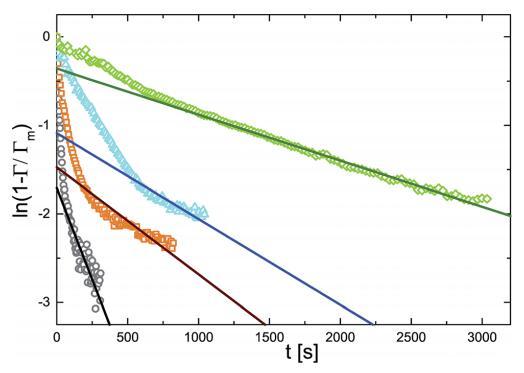
圖 6 ln(1 - r/rm) 作為不同體積濃度的時間函數 微凝膠顆粒:(>)0.10 g l-1 , (D)0.20 克 l-1 , (,)0.50 克 l- 1 , (乙) 1.00 克 l- 1 . 實線是直線擬合。
表 2 不同濃度的速率常數 k(1/s) 值 由圖 6 中的實驗曲線計算

當系統接近飽和時,G(t) 的下降必須 隨著表面變得擁擠,請減速。 的濃度 吸附在表面下方,然后失去平衡 與吸附的物種和動力學受到限制 吸附屏障。 然后一級動力學過程導致:
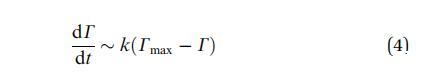
其中,k 是與吸附有關的速率常數 障礙。 理想情況下,k 應該與局部溶質成正比 界面下方的濃度。 這導致指數 松弛:
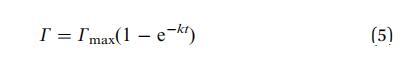
圖 6 表明,這種屏障控制機制確實 確實存在很久了。 空心符號是 ln(1 - G/Gmax) 的實驗值。 在很長一段時間內,曲線擬合一個 用實線表示的直線。 的斜坡 實線可以識別為動力學松弛的倒數 時間為 1/k。
如表 2 所示,速率常數取決于體積 微凝膠顆粒的濃度。 但是依賴是 不是線性的。 這可能表明吸附 過程本身相當復雜,取決于細節 界面上粒子的構型。 更深入的分析 這些方面超出了當前工作的范圍。
微凝膠顆粒在氣液界面處吸附動力學及動態方程研究——摘要、簡介
微凝膠顆粒在氣液界面處吸附動力學及動態方程研究——材料與方法










